(38) The effect of regional bicep brachii muscle volume on angle-specific isometric torque expression

Purpose: The present study aimed to investigate the relationship between joint-specific torque (60°, 90°, 120° flexion) and region-specific muscle volume (MV) (proximal [0%-33%], medial [34%-67%], distal [68%-100%]).

Methods: 15 recreationally trained men (Age = 22.5 yrs ± 3.1; Height = 180.1 cm ± 7.5; Weight  = 77.2 kg ± 13.4) underwent an ultrasonographic assessment of the non-dominant bicep for proximal (15.77 ± 4.05 cm³), medial (18.42 ± 4.16 cm³), and distal (19.53 ± 3.86 cm³) MV, followed by an isometric assessment of maximal voluntary torque capacity (MVIC) at 60° (50.51 ± 12.32 N×m), 90° (65.30 ± 12.80 N×m), 120° (68.03 ± 15.11 N×m) of forearm flexion (180° = full extension). To assess reliability of region-specific MV and angle-specific torque, intraclass correlation coefficients (ICC) were produced using a two-way random effects model. To examine the effects of regional MV on torque, 9, separate, linear mixed effect models were fitted for angle-specific torque with region-specific MV included as fixed effects and random intercepts per participant. For all statistical analysis significance was set at p < 0.05.

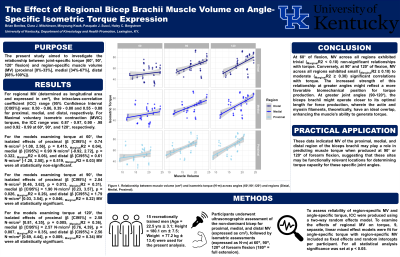
Results: For regional MV, the ICC range (95% Confidence Interval [CI_95%]) was: 0.50 - 0.86, 0.39 - 0.80 and 0.55 - 0.88 for proximal, medial, and distal, respectively. For MVIC torques, the ICC range was: 0.87 - 0.97, 0.90 - .98 and 0.92 - 0.99 at 60°, 90°, and 120°, respectively. For the models examining torque at 60°, the isolated effects of proximal (β [CI_95%] = 0.74 N×m/cm³ [-1.08, 2.56], p = 0.415, _MarginalR² = 0.04), medial (β [CI_95%] = 0.90 N×m/cm³ [-0.92, 2.72], p = 0.322, _MarginalR² = 0.06), and distal (β [CI_95%] = 0.61 N×m/cm³ [-1.28, 2.50], p = 0.519, _MarginalR² = 0.03) MV were all statistically non-significant. For the models examining torque at 90°, the isolated effects of proximal (β [CI_95%] = 2.04 N×m/cm³ [0.46, 3.62], p = 0.013, _MarginalR² = 0.31), medial (β [CI_95%] = 1.90 N×m/cm³ [0.23, 3.57], p = 0.026, _MarginalR² = 0.26), and distal (β [CI_95%] = 1.79 N×m/cm³ [0.03, 3.54], p = 0.046, _MarginalR² = 0.22) MV were all statistically significant. For the models examining torque at 120°, the isolated effects of proximal (β [CI_95%] = 2.58 N×m/cm³ [0.81, 4.35], p = 0.005, _MarginalR² = 0.36), medial (β [CI_95%] = 2.57 N×m/cm³ [0.76, 4.39], p = 0.007, _MarginalR² = 0.35), and distal (β [CI_95%] = 2.56 N×m/cm³ [0.69, 4.44], p = 0.009, _MarginalR² = 0.34) MV were all statistically significant.

Conclusions: At 60° of flexion, MV across all regions exhibited trivial (_MarginalR² < 0.10) non-significant relationships with torque. Conversely, at 90° and 120° of flexion, MV across all regions exhibited small (_MarginalR² ≥ 0.10) to moderate (_MarginalR² ≥ 0.30) significant correlations with torque. The increased strength of this relationship at greater angles might reflect a more favorable biomechanical position for torque production. At greater joint angles (90-120°), the biceps brachii might operate closer to its optimal length for force production, wherein the actin and myosin filaments, theoretically, have an ideal overlap, enhancing the muscle's ability to generate torque. PRACTICAL APPLICATIONS: These data indicated MV of the proximal, medial, and distal region of the biceps brachii may play a role in predicting muscle torque when produced at 90° or 120° of forearm flexion, suggesting that these sites may be a functionally relevant locations for determining torque capacity for these specific joint angles.

Acknowledgements: None